Définitions de Software_for_calculating_π, synonymes, antonymes, dérivés de Software_for_calculating_π, dictionnaire analogique de Software_for_calculating_π (anglais)Where the value of π = 22/7 or 314 Example Convert 90 degrees to radians Solution Given, 90 degrees is the angle Angle in radian = Angle in degree x (π/180) = 90 x (π/180) = π/2 Hence, 90 degrees is equal to π/2 in radian 30 ASCII,Hex,Binary Decimal ASCII text to hex conversion tableThat begin to best f (n) as the values of n become larger For example, g(n) is prime for values of 0 ≤ n ≤ 106 , whereas its famous rival yields primes in this range It has been shown that no polynomial of the form n 2 n q, with q a prime, can do better than the Euler polynomial in giving primes for successive values of n

Unit 1 Whole Numbers
π=22/7 has 1.24 trillion decimal
π=22/7 has 1.24 trillion decimal-The two pieces are placed in a balance, one on each side An additional weight of 11 grams is placed with the smaller piece What is the weight of the small piece?Ezen javult a Kínai matematika különs




Guide To Essential Math By Courtney Williams Issuu
4A car wheel has a radius of 3 ½ dm How many times, to the nearest whole number, will it turn to cover a kilometer? The approximate decimal numbers of these two cuts are 3143 and it was incredibly calculated by Fabrice Bellard to a figure of π 1,24 trillion, * Indeed, this interval is more accurate than 3,14 ˂ π ˂ 22/7 and it was given nearly in 250 years BC Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d) That is, π=c/d This seems to contradict the fact that
Yasumasa Kanada used a 64node supercomputer with 1 terabyte of main memory, to calculate π to roughly 124 trillion digits in around 600 hours There were further sevral records that were made and broken and the latest record of calculating Pi is 224 trillion digits of Pi calculated by Peter Trueb in November 16 using his ycruncher!!!Korai történelem A legismertebb közelítések a következőre π keltezéssel a Common Era előtt két tizedesjegyig pontosak voltak; Techniques of integration 1 SECTION 61 (PAGE 321) R A ADAMS CALCULUS CHAPTER 6 TECHNIQUES OF INTE GRATION Section 61 Integration by Parts (page 321) 1 x cos x dx U = x dU = dx dV = cos x dx V = sin x = x sin x − sin x dx = x sin x cos x C 2
π = 22 7 5Lucy uses about 1 3 kg of laundry soap in 5 days To Professor Yasumasa Kanada, however, pi is an obsession Kanada and a team of researchers set a new world record by calculating the value of pi to 124 trillionIn October 05 they claimed to have calculated it to 124 trillion places 21st century – current claimed world record In August 09, a Japanese Supercomputer called the T2K Open Supercomputer was claimed to have more than doubled the previous record by calculating π to 26 trillion digits in approximately 73 hours and 36 minutes




Pi Day Emma Haruka Iwao Breaks Pi World Record With Google Time




Unit 1 Whole Numbers
Mathematics by experiment Plausible reasoning in the 21st century Experimentation in mathematics Computational paths to discoverySee also chronology of computation of π for a tabular summary See also the history of π for other aspects of the evolution of our knowledge about mathematical properties of π1 league, about 24 miles 1 matchbox volume = 25 mL, Area of the top of a matchbox = cm 2 1 magnum = 2 English wine bottles (2 "reputed" quarts) 1 nail = formerly a weight of 8 pounds or a length of 225 inches 1 peck = 2 dry gallons, a quarter of a bushel



2



Q Tbn And9gcqlkg72qkxjdy3od26wqqzdj0sfpugtfr4wvboxlvb Y5ldc4sc Usqp Cau
Approximations for the mathematical constant pi (π) in the history of mathematics reached an accuracy within 004% of the true value before the beginning of the Common Era In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5tThis is the wiki of "Approximations of π"Most people are ignorant of the fact that a circle has infinite numbers of corners The value of pi is the number of times the diameter of a circle would fit around its circumference The approximate value of pi is 22/7 and it is written as π=22/7 or as π=314 The value of pi with first 100 decimal



A Passion For Mathematics Pdf Free Download



Fundamental Physical Constants Mohr P Taylor B 6 By Marco Acuna Issuu
In November 02, Yasumasa Kanada and a team of 9 others used the Hitachi SR8000, a 64node supercomputer with 1 terabyte of main memory, to calculate π to roughly 124 trillion digits in around 600 hours (25 days) In October 05, they claimed to have calculated it to 124 trillion It would have to be less than , so it must have 0 in the second decimal place as well And it would have to be less than , and so on, and therefore its decimalIn November 02, Yasumasa Kanada and a team of 9 others used the Hitachi SR8000, a 64node supercomputer with 1 terabyte of main memory, to calculate π to roughly 124 trillion digits in around 600 hours (25 days) In October 05, they claimed to have calculated it to 124 trillion



2



2
Background 22 / 7 is a widely used Diophantine approximation of πIt is a convergent in the simple continued fraction expansion of πIt is greater than π, as can be readily seen in the decimal expansions of these values = ¯, = The approximation has been known since antiquity Archimedes wrote the first known proof that 22 / 7 is an overestimate in the 3rd century BCE,Approximations for the mathematical constant pi (π) in the history of mathematics reached an accuracy within 004% of the true value before the beginning of the Common Era (Archi These amateur mathematicians have been called the sufferers of morbus cyclometricus, the circlesquaring disease Stories of these contributors are amusing and at times almost unbelievable Many came close, some went to tens, hundreds, thousands, millions, billions, and now up to ten trillion (10 13) decimal places, but there is no exact




University Physics 13th Edition Solution Manual




Number And Algebra Manualzz
This page is about the history of approximations of π;Pislidespdf Free download as PDF File (pdf), Text File (txt) or read online for freeThe math measurement Pi has been accurately calculated to 124 trillion decimal placesPi Approximation Day is held on July 22 (or 22/7 in day/month date format), since the fraction 22⁄7 is a common approximation of pi (π) 22⁄7 approximation of pi but it not a rational numbers




Interesting Facts About Pi



2
Approximations for the mathematical constant pi (π) in the history of mathematics reached an accuracy within 004% of the true value before the beginning of the Common Era ()In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century Further progress was not made until the 15th centuryThe digits of π have been studied more than any other single constant, in part because of the widespread fascination with and recognition of π Kanada reports that the 10 decimal digits ending in position one trillion are , while the 10 hexadecimal digits ending in position one trillion are 3F341CD5 Changing world views The heptary (base 7) approximation 3 0 6 ˙ = 3 1 equals the famous approximation 22 7 in decimal arithmetic and the quintary approximation of π 3 0 32 ‾ corresponds to the decimal fraction 3 1 5 (3 × 5 2) ∑ k = 1 ∞ 1 5 2 k = 3 17 5 × 1 24



2



2
The number e has the decimal expa nsion Handheld calc ulators typically provide 10 signican t digits of a number be calculated is over 22 trillion!223 / 71 < π < 22 / 7 Before giving an indication of his proof, notice that very considerable sophistication involved in the use of inequalities here Archimedes knew, what so many people to this day do not, that π does not equal 22 / 7 , and made no claim to haveZu Chongzhi is known to have computed π between and , which was correct to seven decimal places He gave two other approximations of π π ≈ 22 ⁄ 7 and π ≈ 355 ⁄ 113 The latter fraction is the best possible rational approximation of π using fewer than five decimal digits in the numerator and denominator Zu Chongzhi's result surpasses the accuracy reached in



2




Daasm608 3rd06fm Mr Hronek Westlake High Manualzz



2



2



2



A Passion For Mathematics Pdf Free Download



2




Even After 22 Trillion Digits We Re Still No Closer To The End Of Pi Fivethirtyeight




Even After 22 Trillion Digits We Re Still No Closer To The End Of Pi Fivethirtyeight



2



2



2




Guide To Essential Math By Courtney Williams Issuu



2




Curious To Know Something New Yes Then This Is The Perfect Place To Grab The Knowledge Do You Know Pi 3 14 Everything About Worlds Most Recognised Mathematical Constant You Need To Know




Hp Calculator Calculator Computer Program
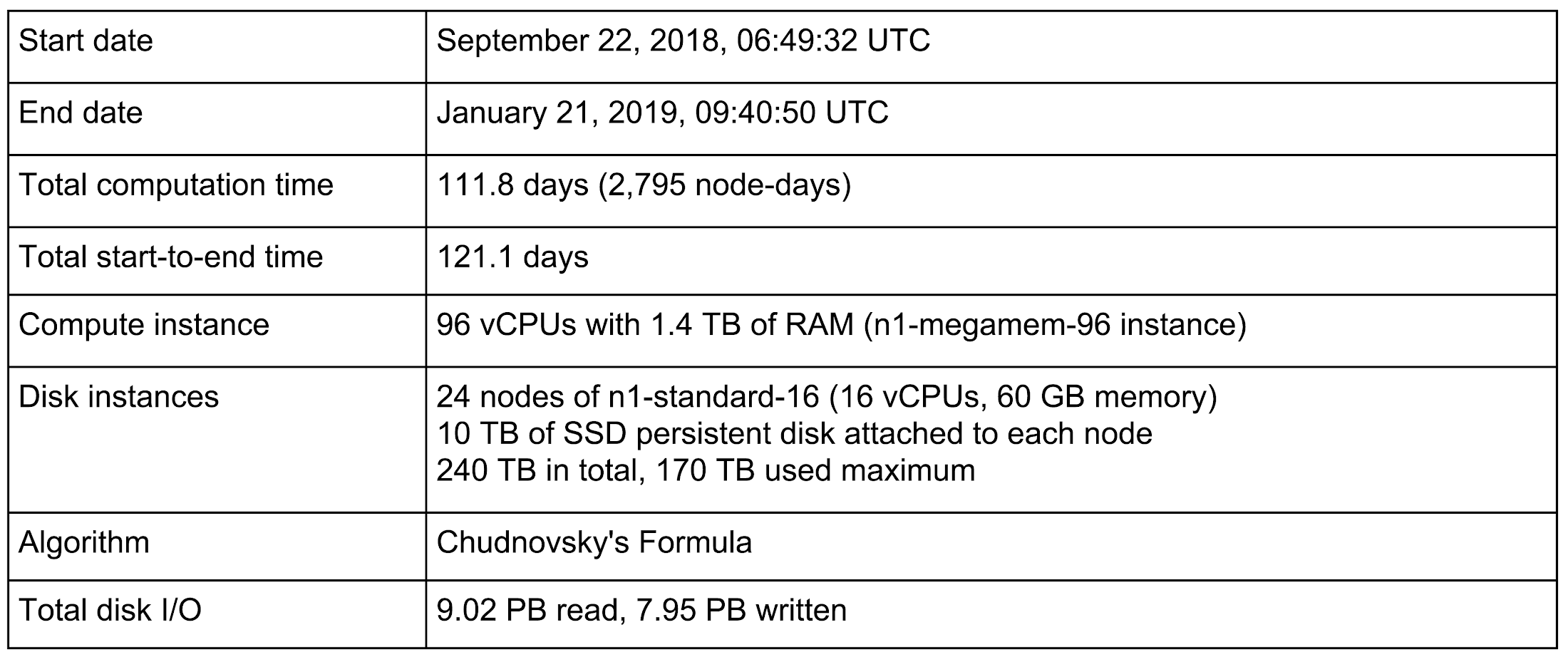



Pi In The Sky Calculating A Record Breaking 31 4 Trillion Digits Of Archimedes Constant On Google Cloud Google Cloud Blog



2




M01 Aircraft Engineering Principles 13 Fraction Mathematics Numbers



2




Explore The Mysterious Number Pi P Stem Little Explorers



2




70 Fun Pi Facts You Definitely Cannot Miss Facts Net



2



2




Number Stories Cipher Calculus



2



2



Q Tbn And9gcq1iddtlxjsrpd6uy0mte8q6lpm80r2q1mbmxzzgulvl8zxtvb8 Usqp Cau




Pdf Part B9 25 Tip As Vt The Total Image Process Alternative Sight Vision Transducer 1sep1965



1 Sinclair N Pimm D Higginson W Eds Mathematics And Aesthetic New Approaches To An Ancient Affinity 07 Springer Pdf




Pi In The Sky Calculating A Record Breaking 31 4 Trillion Digits Of Archimedes Constant On Google Cloud Google Cloud Blog



2



2



2




The Cult Of Pythagoras Math And Myths Pdf Pythagoras Numbers




2 136 2 136 Manualzz




Crazbo Why Is Mathematical Constant Pi So Unique



2




Emma Haruka Iwao Sets Guinness World Record For Most Accurate Value Of Pi Npr




Contents Manualzz



2



2



2



2




Even After 22 Trillion Digits We Re Still No Closer To The End Of Pi Fivethirtyeight



2



2



2




How To Memorize Pi 10 Steps With Pictures Wikihow




Maths You Mayonnaise Pluto



2




Pdf Birth Growth And Computation Of Pi To Ten Trillion Digits



2



2



1



Q Tbn And9gcqllpuvw0f1tgluk6xvmvin Bauonv0i2cnpo7apok Usqp Cau



2



2



2



2



A Passion For Mathematics Pdf Free Download



2



2
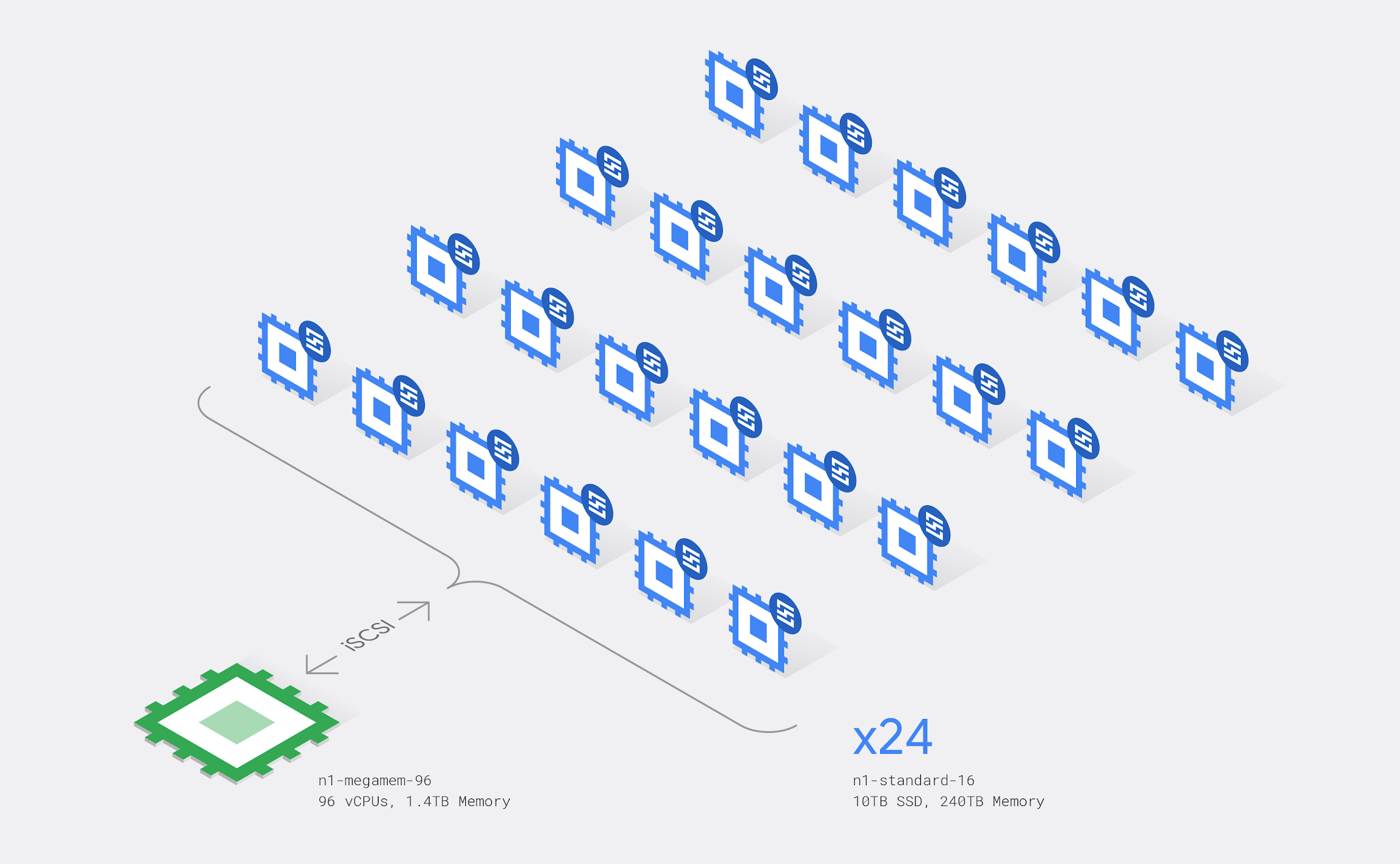



Pi In The Sky Calculating A Record Breaking 31 4 Trillion Digits Of Archimedes Constant On Google Cloud Google Cloud Blog



2




Introduction To Mathematica Complex Number Numbers



2




Math 376 Prealgebra Textbook Fall 10 Version Department Of Mathematics



2




Pi 10 Pi Mathematical Objects



2



2



2



2



2



2



2



2



2



2




Chapter P Prerequisites Manualzz



2




70 Fun Pi Facts You Definitely Cannot Miss Facts Net




The Digital Life Of Pi Pi Fast Fourier Transform



Slac



2




Pi



2



2



0 件のコメント:
コメントを投稿